- The heat balance equation is given by, qi = qo+q1 -Eq (2) Where, qi = Input heat rate from the heater to the copper rod (Watts). Qo = Output heat flow rate from the rod. = Heat flow rate absorbed by water in the cooling water jacket (Watts). Q1= Heat loss from the rod to the surrounding s through thermal insulation, watts (Watts), Assumed to be zero.
- Important even in situations in which there is an intervening medium; a familiar example is the heat transfer from a glowing piece of metal or from a fire. Muddy points How do we quantify the contribution of each mode of heat transfer in a given situation? (MP HT.1) 2.0 Conduction Heat Transfer We will start by examining conduction heat transfer.
Heat transfer takes place as conduction in a solid if there is a temperature gradient
Conduction as heat transfer takes place if there is a temperature gradient in a solid or stationary fluid medium.
With conduction energy transfers from more energetic to less energetic molecules when neighboring molecules collide. Heat flows in direction of decreasing temperatures since higher temperatures are associated with higher molecular energy.
If one end of a metal rod is at a higher temperature, then energy will be transferred down the rod toward the colder end because the higher speed particles will collide with the slower ones with a net transfer of energy to the slower ones.
Conductive heat transfer can be expressed with 'Fourier's Law'
q = (k / s) A dT
= U A dT (1)
where
q = heat transfer (W, J/s, Btu/hr)
k = Thermal Conductivity of material (W/m K or W/m oC, Btu/(hr oF ft2/ft))
s = material thickness (m, ft)
A = heat transfer area (m2, ft2)
U = k / s
= Coefficient of Heat Transfer (W/(m2K), Btu/(ft2 h oF)
dT = t1 - t2= temperature gradient - difference - over the material (oC, oF)
Example - Conductive Heat Transfer
A plane wall is constructed of solid iron with thermal conductivity 70 W/moC. Thickness of the wall is 50 mm and surface length and width is 1 m by 1 m. The temperature is 150 oC on one side of the surface and 80 oC on the other.
The conductive heat transfer through the wall can be calculated
q = [(70 W/m oC) / (0.05 m)] [(1 m) (1 m)] [(150 oC) - (80 oC)]
= 98000 (W)
= 98 (kW)
Conductive Heat Transfer Calculator.
This calculator can be used to calculate conductive heat transfer through a wall. The calculator is generic and can be used for both metric and imperial units as long as the use of units is consistent.
k - thermal conductivity (W/(mK), Btu/(hr oF ft2/ft))
A - area (m2, ft2)
t1 - temperature 1 (oC, oF)
t2 - temperature 2 (oC, oF)
s - material thickness (m, ft)
Conductive Heat Transfer through a Plane Surface or Wall with Layers in Series
The heat conducted through a wall with layers in thermal contact can be calculated as
q = dT A / ((s1 / k1) + (s2 / k2) + ... + (sn / kn)) (2)
where
dT = t1 - t2
= temperature difference between inside and outside wall (oC, oF)
Note that heat resistance due to surface convection and radiation is not included in this equation. Convection and radiation in general have major impact on the overall heat transfer coefficients.
Example - Conductive Heat Transfer through a Furnace Wall
A furnace wall of 1 m2 consist of 1.2 cm thick stainless steel inner layer covered with 5 cm outside insulation layer of insulation board. The inside surface temperature of the steel is 800 K and the outside surface temperature of the insulation board is 350 K. The thermal conductivity of the stainless steel is 19 W/(m K) and the thermal conductivity of the insulation board is 0.7 W/(m K).
The conductive heat transport through the layered wall can be calculated as
q = [(800 K) - (350 K)] (1 m2) / ([(0.012 m) / (19 W/(m K))] + [(0.05 m) / (0.7 W/(m K))])
= 6245 (W)
= 6.25 kW
Thermal Conductivity Units
- Btu/(h ft2oF/ft)
- Btu/(h ft2oF/in)
- Btu/(s ft2oF/ft)
- Btu in)/(ft² h °F)
- MW/(m2 K/m)
- kW/(m2 K/m)
- W/(m2 K/m)
- W/(m2 K/cm)
- W/(cm2oC/cm)
- W/(in2oF/in)
- kJ/(h m2 K/m)
- J/(s m2oC/m)
- kcal/(h m2oC/m)
- cal/(s cm2oC/cm)
- 1 W/(m K) = 1 W/(m oC) = 0.85984 kcal/(h m oC) = 0.5779 Btu/(ft h oF) = 0.048 Btu/(in h oF) = 6.935 (Btu in)/(ft² h °F)
Related Topics
- Heat Loss and Insulation - Heat loss from pipes, tubes and tanks - with and without insulation - foam, fiberglass, rockwool and more
- Steam Thermodynamics - Thermodynamics of steam and condensate applications
- Insulation - Heat transfer and heat loss from buildings and technical applications - heat transfer coefficients and insulation methods and to reduce energy consumption
- Thermodynamics - Effects of work, heat and energy on systems
Related Documents
- Acetone - Thermophysical Properties - Chemical, physical and thermal properties of acetone, also called 2-propanone, dimethyl ketone and pyroacetic acid. Phase diagram included.
- Ammonia - Prandtl Number - Figures and table showing changes in Prandtl number for ammonia with changes in temperature and pressure
- Ammonia - Thermal Conductivity at Varying Temperature and Pressure - Online calculator, figures and tables showing thermal conductivity of liquid and gaseous ammonia at temperatures ranging -70 to 425 °C (-100 to 800 °F) at atmospheric and higher pressure - Imperial and SI Units
- Arithmetic and Logarithmic Mean Temperature Differences in Heat Exchangers - Arithmetic Mean Temperature Difference - AMTD - and Logarithmic Mean Temperature Difference - LMTD - formulas with examples - Online Mean Temperature Calculator
- Benzene - Thermophysical properties - Chemical, physical and thermal properties of benzene, also called benzol. Phase diagram included.
- Butane - Thermal Conductivity - Online calculators, figures and tables showing thermal conductivity of liquid and gaseous butane, C4H10, at varying temperarure and pressure, SI and Imperial units
- Carbon dioxide - Thermal Conductivity - Online calculator, figures and table showing thermal conductivity of carbon dioxide, CO2, at temperatures ranging from -50 to 775 °C (-50 to 1400 °F) at atmospheric and higher pressure - Imperial and SI Units
- Convective Heat Transfer - Heat transfer between a solid and a moving fluid is called convection. This is a short tutorial about convective heat transfer
- Cooling Mode - Heat Flux - Heat fluxes for various cooling or heat transfer modes
- Cylinders and Pipes - Conductive Heat Losses - Conductive heat losses through cylinder or pipe walls
- Energy Transfer Equation - Fluid energy transfer
- Ethane - Thermal Conductivity - Online calculator, figures and table showing thermal conductivity of ethane, C2H6, at varying temperature and pressure - Imperial and SI Units
- Ethylene - Thermal Conductivity - Online calculator, figures and table showing thermal conductivity of ethylene, also called ethene or acetene, C2H4, at varying temperature and pressure - Imperial and SI Units
- Ethylene - Thermophysical Properties - Chemical, physical and thermal properties of ethylene, also called ethene, acetene and olefiant gas. Phase diagram included.
- Food - Thermal Conductivity - Thermal conductivity of selected foodstuff
- Fouling and Reduced Heat Transfer in Heat Exchangers - The heat-transfer in a heat exchanger is reduced by fouling
- Hydrogen - Thermal Conductivity - Online calculator, figures and table showing thermal conductivity of hydrogen, H2, at varying temperature and pressure - Imperial and SI Units
- Insulation Materials - Temperature Ranges - Temperature limits for some commonly used insulation materials
- International Standard Atmosphere - International standard atmosphere in elevation -2000 to 30000 metre - pressure, temperature, density, viscosity, thermal conductivity and velocity of sound
- Methane - Prandtl number - Figures and table showing changes in Prandtl number for methane with changes in temperature and pressure
- Methane - Thermal Conductivity - Online calculator, figures and table showing thermal conductivity of methane, CH4, at temperatures ranging from -160 to 725 °C (-260 to 1300 °F) at atmospheric and higher pressure - Imperial and SI Units
- Nitrogen - Prandtl number - Figures and tables showing Prandtl number of nitrogen at varying temperarure and pressure, SI and Imperial units
- Nitrogen - Thermal Diffusivity - Figures and tables showing thermal diffusivity of nitrogen at varying temperarure and pressure, SI and Imperial units
- Overall Heat Transfer Coefficient - Calculate overall heat transfer coefficients for walls or heat exchangers
- Plastics - Thermal Conductivity Coefficients - Thermal conductivity of plastics
- Propane - Prandtl Number - Figures and tables showing Prandtl Number of liquid and gaseous propane at varying temperarure and pressure, SI and Imperial units
- Propane - Thermal Conductivity - Online calculator, figures and tables showing thermal conductivity of liquid and gaseous propane at varying temperarure and pressure, SI and Imperial units
- Steel Pipes Heat Loss Diagram - Heat loss from steel pipes and tubes - dimensions ranging 1/2 - 12 inches
- Thermal Conductivities of some common Liquids - Some fluids and their thermal conductivities
- Thermal Conductivity Conversion Factors - Convert between thermal conductivity units
- Thermal Conductivity of Metals, Metallic Elements and Alloys - Thermal conductivity of common metals, metallic elements aand Alloys
- Thermal Conductivity of some selected Materials and Gases - Thermal conductivity of some selected gases, insulation products, aluminum, asphalt, brass, copper, steel and other common materials
- Thermal Conductivity Online Converter - Convert thermal conductivities
- Thermal Resistivity and Conductivity - Thermal resistivity and conductivity
- Thermal Transmittance and Thermal Resistance - Thermal transmittance U and thermal resistance R
- Thermoplastics - Physical Properties - Physical properties of some thermoplastics like ABS, PVC, CPVC, PE, PEX, PB and PVDF
- Water - Thermal Conductivity - Figures and tables showing thermal conductivity of water (liquid and gas phase) with varying temperature and pressure, SI and Imperial units
Tag Search
- en: conduction heat transfer temperature
- es: conducción de la temperatura de transferencia de calor
- de: Leitungswärmeübertragungstemperatur
Science >Physics >Heat Transfer > Conduction
Heat always gets transferred from the body and higher temperature to a body at lower temperature heat transfer can take place in three ways a) Conduction b) Convection and c) Radiation. In this article, we shall study the heat transfer by the conduction.
Conduction:
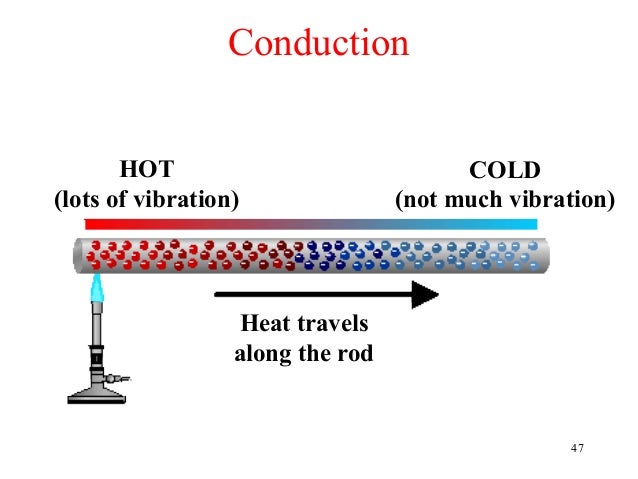
If one end of a metal rod is heated, the other end also gets heated up. This is due to conduction. When one end of a metal rod is heated, the kinetic energy of the molecules at that end increases. The molecules start vibrating with a higher amplitude. These molecules start vibrating with a higher amplitude. These molecules during vibration collide with the neighbouring molecules and transfer part of their energy to the neighbouring molecules. Thus the kinetic energy of the neighbouring molecules increases hence their amplitude of vibration increases and during the collision the energy transfers to the next molecule. Thus heat transfer takes place by conduction.
The modeof heat transfer between two parts of a body or between two bodies in contactwhich are at different temperatures without actual migration of particles ofthe body is called conduction.
Dependingupon easiness of heat transfer by conduction the substance are classifieds intotypes a) Good Conductors and b) Bad conductors
Good Conductors:
Thesubstances which allow the heat to pass through them very easily are calledgood conductors. Examples. Aluminum, copper, Silver, Steel, Bronze, Brass, allmetals
Bad Conductors:
Thesubstances which do not allow the heat to pass through them are called badconductors. Bad conductors of heat are also called as insulators. Examples:wood, rubber, Plastic, paper, glass, air, ebonite , bakelite.
Heat Transfer In Metal Rod Art
Use of conduction:
- Metals are used for making utensils because the metals are good conductors of heat they allow heat to pass through them easily.
- Cooking vessels have plastic handles because plastic a bad conductor of heat it does not allow the heat to pass through from hot vessel to hands and thus danger of burning can be avoided.
- Tea-cups, Teapots, coffee jugs are made of porcelain.
- Mountaineers use sleeping bags in polar regions.
- People wear woolen cloth in winter.
- Nowadays cooking vessels are made with copper bottoms.
- In winter, the metal lock feels colder than the wooden door on touch.
Characteristics of conduction:
Heat Transfer In Metal Rods
- In this type of heat transfer, there is no actual migration of the medium particles from one point to another.
- For conduction, there must be a material contact between the two bodies.
Concept of Steady-State and Temperature Gradient:
Heatconduction may be described quantitatively as the time rate of heat flowin a material for a given temperature difference.
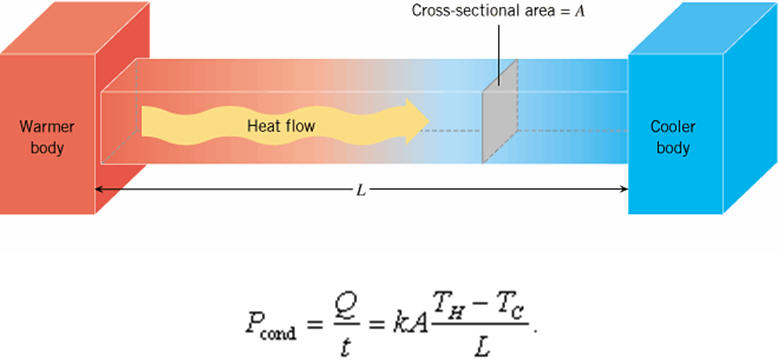
Consider ametallic bar AB of length L and uniform cross-sectional area A withits two ends maintained at different temperatures. The temperaturedifference between the ends can be obtained by keeping the ends in thermalcontact with large reservoirs having temperature differences. Some holesare drilled on this rod to insert thermometers (say T1, T2,T3, and T4) in the rod. For better thermal contactbetween the rod and thermometers mercury is poured into the holes. The sides ofthe bar are fully insulated so that no heat is exchanged between thesides and the surroundings.
Let θ1, θ2, θ3, and θ4 be the temperatures recorded by the thermometers T1, T2, T3, and T4 respectively. Initially, the temperature rises and after some time every thermometer shows its own constant reading such that (θ1 > θ2 > θ3> θ4). This state is called the steady-state.
Due to the insulation of the rod, no heat is lost due to surroundings. At a steady-state, at every cross-section of the rod, the quantity of heat entering the section in one second is equal to the quantity of heat leaving the section due to conduction.
Let usconsider two sections separated by distance Δx and let Δθ be thetemperature difference between these two sections. then the quantity Δθ/ Δx is called the temperature gradient.
The temperature gradient is defined as the rate of change of temperature with the distance when the material is in steady-state.
Thermal Conductivity:
It is found experimentally that in this steady state, the rate of flow of heat (or heat current)H is proportional to the temperature difference (θ2 – θ1) and the area of cross-section A and is inversely proportional to the length L
Where K = Constant called the thermal conductivity or the coefficient of thermal conduction the material. The greater the value of K for a material, the more rapidly will it conduct heat.
The SI unitof K is J S–1 m–1 K–1 (jouleper second per metre per kelvin) or W m –1 K–1 (wattper metre per kelvin).
The value ofthermal conductivity varies slightly with temperature but can be considered tobe constant over a normal temperature range. Good thermal conductors havevery high values of thermal conductivity while thermal insulators havenegligible values of thermal conductivity.
Houses made of concrete roofs get very hot during summer days because the thermal conductivity of concrete (though much smaller than that of metal) is still not small enough. Therefore, a layer of earth or foam insulation is put on the ceiling so that heat transfer is prohibited and the room remains cooler.
Searle’s Experiment:
Apparatus:
Apparatusconsists of the thermally insulated box housing a metallic bar of auniform cross-sectional area with its one end kept in contact withsteam in a steam chamber. Two holes are drilled to insert thermometers T1 and T2,in the rod separated by distance x. For better thermal contact between the rodand thermometers mercury is poured into the holes. Cooling water is circulatedaround the rod whose initial and final temperatures are measured by thethermometers T3 and T4.
Working and Calculations:
At steady state, the heat lost by rod = heat gained by the water
Where, mW = Mass of water, SW =Specific heat of water, t = time for which heat is flowing
Measuring all values on R.H.S. of the formula value of K canbe found.
Values of thermal conductivity in J S–1 m–1 K–1 fordifferent materials are given below